黎曼猜想，作为数学领域的一大未解之谜，长久以来吸引了全球数学家的关注，其深奥的特性和潜在的价值使得这一猜想成为数学研究的重要课题，随着科学技术的不断进步和数学研究的深入，黎曼猜想的最新发展进程也取得了重要的突破，本文将详细介绍黎曼猜想的最新发展进程，探讨其未来的研究方向。

黎曼猜想的概述

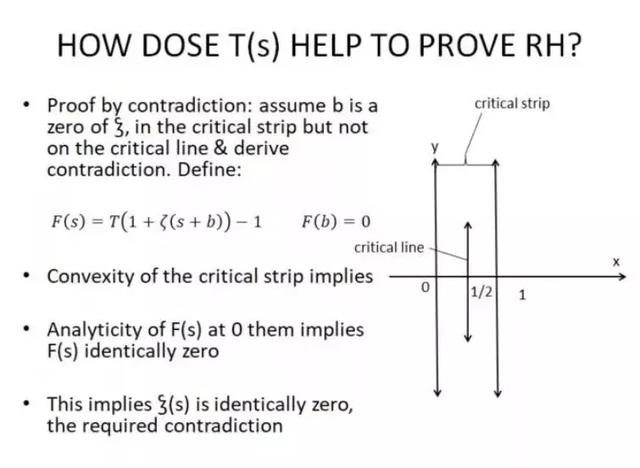
黎曼猜想源于数学大师黎曼提出的黎曼假设，其主要涉及素数分布和黎曼ζ函数，这一猜想的核心问题是探究黎曼ζ函数的非平凡零点与素数的分布之间的关系，由于其对数学领域的重要性，黎曼猜想一直是数学家们竞相研究的热点。

黎曼猜想的最新发展进程

近年来，黎曼猜想的研究取得了显著的进展，以下是一些关键的发展：

1、新的研究方法：随着数学研究的深入，数学家们不断探索新的方法来研究黎曼猜想，通过引入新的函数空间、概率论和随机矩阵理论等工具，为黎曼猜想的研究提供了新的视角。

2、数值验证：通过高性能计算机进行大规模的数值计算，数学家们已经对黎曼猜想的部分结论进行了验证，这些验证工作为理解黎曼猜想的真实性提供了重要依据。

3、理论突破：在理论方面，数学家们取得了诸多突破，对黎曼ζ函数的性质进行了深入研究，揭示了其与素数分布之间的更深层次的关系，一些新的猜想和模型也被提出来，为黎曼猜想的研究提供了新思路。

4、跨学科合作：越来越多的数学家与其他领域的专家进行合作，共同研究黎曼猜想，这种跨学科合作有助于引入新的观点和方法，推动黎曼猜想的解决。

最新研究成果与进展

在黎曼猜想的最新研究中，以下是一些重要的成果与进展：

1、零点分布的研究：数学家们对黎曼ζ函数的非平凡零点的分布进行了深入研究，取得了一系列重要成果，这些成果有助于揭示素数的分布规律，为黎曼猜想的研究提供了重要线索。

2、素数定理的改进：基于黎曼猜想的研究成果，一些素数定理得到了改进和完善，这些定理对于理解素数的分布具有重要意义，有助于推动黎曼猜想的研究。

3、计算机辅助证明：随着计算机技术的发展，一些数学家尝试利用计算机辅助证明黎曼猜想，虽然这些尝试尚未取得最终突破，但为证明黎曼猜想提供了新的可能性。

未来研究方向

尽管黎曼猜想的研究已经取得了重要进展，但仍有许多问题需要进一步探讨：

1、新的理论框架：数学家们需要探索新的理论框架，以更深入地理解黎曼ζ函数和素数的分布关系。

2、实验验证与数值模拟：通过高性能计算机进行更大规模的数值计算，进一步验证黎曼猜想的结论。

3、跨学科合作：加强与其他学科的合作，引入新的观点和方法，共同攻克黎曼猜想。

4、其他相关问题的研究：除了黎曼猜想本身，数学家们还需要关注与之相关的其他问题，如素数定理、孪生素数猜想等，这些问题的研究有助于推动黎曼猜想的研究进程。

黎曼猜想的最新发展进程取得了重要的突破和成果，尽管仍面临许多挑战，但随着数学研究的深入和跨学科合作的发展，我们相信黎曼猜想终将得以解决。